Methods
Density Functional Theory & Molecular Dynamics
The complexity of the many-body Schrödinger equation for a system of interacting electrons makes it impossible to approach its solution in a straightforward way. A certain set of assumptions, simplifications and other approximations must be used to obtain a reasonable description of the electronic structure of a complex system. Besides the traditional Hartree-Fock pathway, density functional theory (DFT), founded by P. Hohenberg and W. Kohn, has emerged in the last decade as the method of choice, since it enables the calculation of increasingly large systems at a moderate computational cost, together with a sufficient accuracy.
Density Functional Theory & Molecular Dynamics
In DFT, the electronic structure is represented by a set of independent wavefunctions. They are the solution of a single-particle Schrödinger equation, governed by the electrostatic potential created by the total electronic density of all these wavefunctions. The complicated quantum-mechanical restrictions of the “true” electronic wavefunction, such as exchange and correlation effects, are taken into account by means of a further potential energy term, the exchange-correlation potential. It is made such that physical properties of the total electronic density are reproduced as good as possible. Unfortunately, this exchange-correlation potential is not unique. There is a whole theory behind it, and many variants have been proposed for the exact shape of this potential. So far, there seems to be no optimal way of expressing exchange and correlation effects within DFT. However, for the most common choices of this particular element, density functional theory has shown to yield very useful predictions of the properties of matter, and it is becoming more and more popular.
Molecular Dynamics means the numerical time-integration of Newton's equations of motion. In particular, this can be done for a system of atoms, which interact directly and by means of their electrons. The total force felt by an atom is determined by the surrounding atoms as well as the electronic structure. The combination of density functional theory with molecular dynamics techniques, as pioneered by R. Car and M. Parrinello, enables the direct observation of microscopic processes through the calculation of atomistic trajectories.
Nuclear Magnetic Resonance
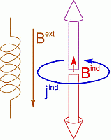
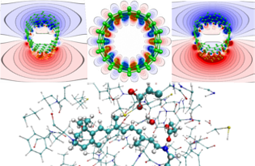
Nuclear Magnetic Resonance (NMR) deals with the phenomenon that in a magnetic field, nuclear spins have discrete, quantized energy levels. The energy difference between these states depends on the local magnetic field at the position of the nucleus. Apart from the externally applied magnetic field (Bext), there is an additional contribution to the local field (Bind), due to the response of the electrons around the atom (jind). This response is of quantum-mechanical nature, but often it is referred to as “ring currents”. They are determined by the specific electronic structure in the neighborhood of the considered nucleus and give characteristic information of its chemical environment. The additional field induced by those currents is anisotropic, so that different orientations of identical molecules result in different local fields for their atoms.

Modern experiments measure the precession frequency of the nuclear spin rather than the energy levels directly. In their ground state, the spins are aligned along the quantization axis of the magnetic field. Upon irradiation with suitable radio-frequency pulses, they are “flipped” into a plane orthogonal to the external field, in which they start precessing with a characteristic frequency (the Larmor frequency) which is proportional to the local magnetic field. Subsequently, they fall back to their all-aligned state during a characteristic relaxation time. The experimental detection of the Larmor frequency is performed by a Fourier transformation of the free induction decay of the electromagnetic field emitted by the precession motion. From the precession frequency, one can obtain the local magnetic field at the position of the nucleus. There are numerous excellent textbook about the elementary interactions between nuclear spins and electrons in magnetic fields that describe this procedure extensively on the quantum-mechanical level.
Nuclear Magnetic Resonance 3
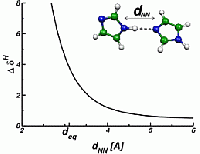
The change in the resonance frequency of a given nuclear spin with respect to a reference spin of the same type is called NMR chemical shift δ. It is given by the dimensionless proportionality tensor between the induced part of the local magnetic field and the homogeneous external field, and the typical order of magnitude of this quantity is ppm (parts per million, 10-6). The spectrum of these chemical shifts represents a fingerprint of all spins of the system and can be used to obtain valuable insight into microscopic structure. The information that is nowadays routinely extracted from NMR experiments ranges from the atomic bonding characteristics (bond lengths and bond angles) over the characterization of hydrogen bonding networks up to packing effects on the supramolecular and macromolecular level. On the right, the dependence of the proton NMR chemical shift on the distance of an imidazole dimer is illustrated.
CPMD: Car-Parrinello Molecular Dynamics
CPMD means both the general Car-Parrinello Molecular Dynamics method and a particular computer simulation code that is based on this approach. The CPMD code is a popular density-functional-theory based code that relies on the plane-wave basis set and pseudopotentials to screen the core electrons.
CP2K
CP2K is a newer code that is also developed in the Parrinello-family. Inside CP2K, there is a classical and a density functional module. The latter is based on a mixed basis which uses Gaussian basis functions for the representation of the electronic orbitals, but plane waves for the description of the electronic density.